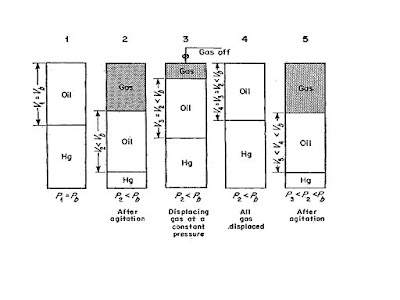
LEY DE POISEUILLE PARA FLUJO CAPILAR.

Aunque los espacios porosos de las rocas no se asemejan a tubos capilares rectos, de paredes suaves y diámetro constante, es práctico e instructivo considerarlos como si consistiesen en manojos de tubos capilares de diferentes diámetros. Considérese un tubo capilar de L cm de longitud y ro de radio interior a la cual a través del cual avanza un fluido de µ poises de viscosidad en un flujo laminar o viscoso bajo una presión diferencial de (p1 – p2) dinas por cm2. Si el flujo humedece las paredes del capilar, la velocidad allí será cero y aumenta a su máximo en el centro. El flujo se puede visualizar como una serie de superficies parabólicas concéntricas moviéndose a diferentes velocidades y, por consiguiente, ejerciendo fuerzas viscosas entre si se puede expresarse por la relación.

F= µ*A*dV/dx

Donde µ esta en poises, A en cm2 y el gradiente de velocidad dv/dx en cm/seg/cm y la fuerza F en dinas. Por consiguiente, la fuerza viscosa sobre un tubo o cilindro de r cm de radio es:

Fv = µ*A*dV/dx= µ*(2πrL)*dv/dr

La fuerza de desplazamiento sobre este mimo tubo es la presión diferencial de (p1 – p2) que actúa sobre el área πr2, o (p1 – p2) πr2 dinas. Si el fluido no se acelera, la suma de las fuerzas desplazante y de retardo viscoso será cero y

µ *(2πrL)*dv/dr + (p1 – p2) *πr2 =0

Integrando,

dv=- (p1 – p2) r*dr/2 µ*L + C1

La constante de integración C1 se puede evaluar considerando v=0 a r= ro, o C1= ro2*(p1 – p2)/4*π*L. luego:

V= (ro2-r2)* (p1 – p2)/4 µ*L

Esta expresión de la velocidad de cualquier superficie cilíndrica de radio r, e indica que la velocidad, parabólicamente desde un máximo en el centro a cero en las paredes, como lo muestra la figura siguiente:

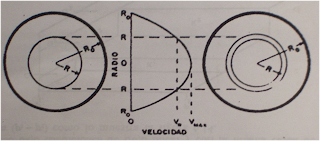
Distribución de la velocidad en flujo capilar viscoso (laminar).

La rata volumétrica de flujo a través del elemento de espesor dr es dq= v*Da, donde el area Da=2πdr. Luego la rata de flujo total a través del tubo es la integral de estos flujos elementales individuales o:

ecuacion 6.19.

Esta expresión es denominada ley de Poiseiulle para flujo laminar (viscoso) de líquido a través de tubos capilares. La rata de flujo de un fluido de 0.015 poises a través de un capilar de 0.10 cm de radio, 25 cm de largo y bajo una presión diferencial de 300 dinas por cm2 es:

Q= 3.14*(0.10)4*300/8*0.015*25=0.0314 cm3/s.

Klikenberg dedujo una ecuación similar a la ecuación anterior (6.19) para flujo de gas, asumiendo una velocidad finita de deslizamiento del gas en la pared del tubo capilar, ya que el gas no es una sustancia humectante. Comparando las dos ecuaciones, puede concluirse que la permeabilidad de los gases es mayor que la de los líquidos, y la diferencia se acentúa para rocas de menor permeabilidad, menores presiones medias de flujo de gas y menores pesos moleculares de los gases. En el laboratorio se han obtenidos medidas de permeabilidad al aire a una presión media de dos atmosferas, entre 1.0 y 100 mD, mostrando los resultados aumentos sobre la permeabilidad del liquido, desde porcentajes muy bajos hasta el 100 por ciento. Como el efecto varia inversamente con la presión media del gas, es de poca importancia a las presiones comunes de los yacimientos.

La ley de Darcy para el flujo lineal de líquidos en capas permeables y la ley de Poiseiulle para el flujo capilar de líquidos son bastante similares. La ley de Darcy expresada en términos de cm 3 por segundo, poises, cm, dinas por cm3 y Darcys es:

Q=9.86*10-9*KA*(p1 – p2)/µ*L

Escribiendo A= π r2 para el área en la expresión de la ley de Darcy, e igualándola a la ecuación (6.19)

K=12.7*104*r3, Darcys.

Por lo tanto la permeabilidad de una roca compuesta de tubos capilares compactamente empacados, de 0.0001 pulgada en diámetro es cerca de 0.20 D O 200mD. Y si solo 25 por ciento de la roca son canales porosos la permeabilidad será solo la cuarta parte o cerca de 50 mD.

Fuente: B.C. Craft y M.F Hawkins.